|
Theory & Practice - Issue 05 - Landscapes by (05 July 2000) |
Return to The Archives |
Introduction
 |
|
I'd like to thank you guys for your responses to my Intermediate Issue 4.5.
Among other things, I've received quite a few emails from readers who were
enthuastic about my writing an issue on landscape engines. I have had to pause
my writing this column due to being very busy with a host of other things. But
in the meantime I have thought about the topic and what I want to present.
Landscapes are a big topic to cover, and I will spend at least 2 issues on it. Why are landscapes all the rage with some people? Well, I suppose, for different reasons. First, if done right they can look really nice. Second, generating landscape data, either through an editor or by other means, is easier than for other types of environments, such as indoors. So pretty much, once you have an engine you can go and quickly make tests for it. Once your engine reaches an advanced state, you can make good looking demo maps to show to everyone :-) |
In General
 |
| Landscape is of a nature quite different from other types of things, such as the insides of buildings. If we assume some things about the nature of a landscape we can come up with good ways of modeling it, which are both efficient and versatile. Generally, we store a landscape using one or more heightmaps. A heightmap records the height of the landscape at evenly spaced points, so you get a 2-dimensional grid filled with height values. For a landscape that has only one height at any point, one heightmap is all we really need to store. This is a small restriction, because you can make a lot of great-looking landscapes that don't have parts hanging over other parts. In fact, most landscapes don't have that. |
Interpreting The Data
 |
|
So you are representing the landscape with a heightmap. The heightmap is, of
course, of finite size. That means you will not be storing the height of every
point on the landscape, but instead the heights of evenly spaced points. To have
a continuous surface for the landscape, we will have to have some sort of
transitions between these points. Static height - This method basically just takes the height specified at a grid point and uses it as the height for the whole heightmap cell that point represents. It connects heights by using vertical bars. So it looks like a staircase or some kind of bar graph. Not very realistic. Linear interpolation - With this method, you interpolate the height linearly between the points. It is as if you had a quad for each cell in the grid whose vertices were the four points around the cell. There is a big chance that the quad won't be planar, so instead of having a quad you split it into two triangles. The results are a bit different depending on how you split it, but you should split every quad from the map the same way. That way you can generate triangle strips and other nice stuff (more on that later). Curved surfaces - These can come in handy when you to have smooth transitions. Remember that with curved surfaces you can vary the level of detail, so you can tesselate a lot up close and less as you get further, until you switch to linear interpolation. I will discuss this in more detail later, but generally this addition is slower but more flexible. In general we can call curved surfaces here interpolation of higher than linear order. |
Bringing Out The Details
 |
Now, if you had just implemented a simple algorithm that would read a heightmap,
connect the points using triangles (linear interpolation), and send these
triangles to the rasterizer, you'd already have a simple engine that could draw
basic landscape. The heightmap points would be spaced evenly in squares, and the
resulting top view of your landscape would look something like: This is already pretty good for a basic landscape. But we're just getting started. Here is our first problem: when you render this landscape up close you will see that it seems a bit jerky and lacks realistic detail. If you want more detail in the landscape you'll have to place the heightmap's points closer together. But then you will have a lot more triangles to render overall, because you'd be increasing the detail on the entire map! (Perhaps one day we will have computers so fast we won't care about this, but as I write, we don't.) Instead, we want to have a system where the landscape would be rendered with more detail up close, but further away it should have less and less detail. One way to do it is have mipmapped heightmaps -- several versions of the same heightmap, with different detail. But that usually isn't a good solution because it still doesn't give you a big enough LOD range, and takes up a lot of space in memory. Rather, what we want can be done using progressive mesh techniques. For a progressive map, you would have a basic map with a constant level of detail, but also store information for various sections of the map which will increase the detail according to a detail level specified. Then when time comes to render, you try render the close-up polygons with a high level of detail. This will attempt use the information for increasing detail that is contained in the map for that section. If there is enough information to match the LOD chosen, that amount of detail will beused. Otherwise the closest amount of detail to the chosen LOD will be used. As you go further away you lower the LOD requirement until it drops to the default detail. 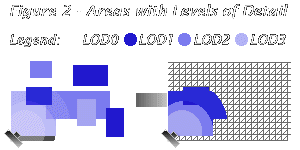 In short, you have information on how to increase details in sections of the map given a certain detail level, and when you're moving around the map with a camera you specify high detail levels close to the camera and lower levels further away. Now, we will explore how that information is stored. There are various algorithms for storing progressive landscape maps, such as the quadtree. However, you've probably noticed that I like to write about things from a different point of view, or present new techniques. Why duplicate something which has already been written? If you want information on standard quadtree techniques you can check out the links section at the end. So, in this case, we'll develop our own method of storing and using progressive heightmaps. We'll have our basic heightmap, split up into triangles as usual, but some triangles might contain further detail. This detail is achieved using the structure Face. Imagine a Face to be a triangle facing outward from the landscape. This Face might be split into 3 faces, by introducing an extra vertex.  We can define our structure like this:
Let's take a look at what this means. Details is a pointer to an array of 3 faces into which the face can split. If it is NULL, then no more detail can be achieved. (Notice the recursion -- struct Face contains a member of type Face*... we use recursion to implement progressive meshes because we split faces recursively). Tip is the vertex that's used to split the face into 3. It's the tip of the pyramid that results. Let's forget about the landscape for a moment and focus on how we're going to implement drawing in this progressive detail scheme. Suppose we had a triangle (3 vertices) and a Face pointer. If we were to write a function that took face, a level of detail and sent primitives to the rasterizer, it would look something like:
Since we have a triangle (3 vertices) and a face pointer corresponding to that triangle, we would draw the thing as follows. First we'd fill the V array with the vertices from the polygon, then call the Draw function of the face with the LOD we wanted. When it returns, the face would have been drawn with that level of detail, or as much detail as could have been mustered to match. DrawFan and DrawTriangle are functions that do the actual drawing. Functions like that can be found in APIs like OpenGL or DirectX. Using this method, we can draw our landscape, adjusting the level of detail depending on distance. For the triangles which are up close we would call Face::Draw with a high LOD. As we move further away we will call it with smaller and smaller LOD, until the LOD drops to 0. When the LOD is 0, we could continue calling Face::Draw(0), but that would draw each triangle individually. Since now the level of detail is minimal we can just send the triangle strips instead! Notice how in the basic heightmap the squares are split into triangles in such a way as to allow triangle strips to be formed easily. Thus they can be sent to the rasterizer all at once. So far away you can draw a lot of terrain quickly, but take your time up close, where you're not drawing polygon strips, but instead filling in the detail. |
Storing Progressive Maps
 |
|
Okay, back to our landscape. Now that we know how to draw our progressive
meshes, we should also figure out how to store them. We already know that the
basic heightmap is stored as a 2D array (grid) of heights. Each square from that
grid is divided into 2 triangles. Each triangle can potentially have a Face
structure attached to it. But usually not all will. In fact, most probably
won't. Say you're making a game where you drive along a road in the countryside. Here you can restrict where the camera will be (or at least assume where it will usually be). In this case it's in the vicinity of the road. So, you can store nice detail on the road and around it (rocks, crevices, rough hills, landslides, etc.), but for the rest of the map you will simply have the default detail that the heightmap allows. In this case, a small part of your map will have details. If, instead, you're making a game where you can go anywhere and do anything, you still probably won't want to make every section of the map very detailed. A large percentage of the map will have default detail. In this case, it is wasteful to have, along with the NxN heightmap, a 2NxN array of Face pointers. If most of the map has default detail, most of the entries in the Face pointer array will be NULL. So we might try and come up with a more space-saving scheme for storing Face pointers for appropriate triangles. One such scheme is as follows. You have your heightmap as a 1-dimensional array. The [x][y] are turned into [x+y*width].
Then you also have an array (1-dimensional) of Faces, sorted in the order that their pointers would have been sorted in the 2NxN array. But in this array you don't have all 2N2 elements, since large portions of the map are not detailed. Instead, it is as if you were storing the Faces in order they would otherwise be stored, but skipping some as you go.
Now comes the interesting part. You also store a sorted array of integers, with the same number of elements as the Faces array. Element number X of the array holds the index of the triangle in the Heights array that associates with element number X of the faces array.
What we've actually done here is this: instead of using the array of triangles and storing an array of corresponding pointers to Faces, we've got an array of Faces and storing an array of corresponding pointers to triangles. Now, how do we take advantage of this as we're drawing? Well, as we draw a particular triangle we find whether or not it has a corresponding Face by searching the Triangles array for the index of the triangle we're processing. This might seem computationally more expensive, but it's really very bad: since the Triangles array is sorted, we can use a binary search, which will produce its results in at most (log2n)+1 steps. So for 1,000,000 elements you'll need 20 steps. Moreover, if you're processing the triangles sequentially (as you probably will when you're drawing the heightmap), you could have interesting optimizations. Say you start processing triangles from the beginning. You can check the Triangles array for the value of the first element, x1=Triangles[0]. Now you know there are no detailed triangles up to that x1. So you can just draw a triangle strip up to triangle x1 and save time. Then once you reach that triangle, you find the value of the next element of the Triangles array, x2 = Triangles[1]. Draw the triangle with the appropriate LOD (by calling Face::Draw) and then draw another triangle strip for all the triangles between x1 and x2... and so on, until your LOD drops to 0, in which case you don't have to consult the Faces array anymore for that frame, just draw triangle strips for the rest of the triangles in the scene. |
Generating Landscape
 |
|
The progressive maps we've seen so far have all had their detail stored
beforehand. The basic heightmap and detail could have been generated by artists
with a lot of time on their hands, or by an external computer program, but in
any case it would have to be stored in its entirety somewhere -- either in RAM,
or on a HD, etc. Alternatively, instead of storing information for a progressive mesh, you can generate one programmatically. In this case you can have very large maps, and in most cases increase level of detail indefinitely, but the results aren't totally specified by you. Rather, they are obtained by some algorithm. There are many algorithms that do this sort of thing. Most that produce realistic looking landscapes are fractal-based. They make big changes on a large scale, and then make smaller and smaller details. This reflects what usually happens in nature -- as the scale gets smaller, so does the severity of the changes. Some algorithms want you to provide them with a series of parameters affecting how they will generate the landscape. Perhaps some random seeds, a few basis coefficients, and that's it. Some algorithms are more interactive, and give you this in addition to letting you specify your own "rough" heightmap, so you can have control over where approximately you want valleys, moutaineous regions, plains, craters, etc. Below, I'll talk about an algorithm of the latter kind. Biquadratic Surfaces with Progressive Deformations That's the rather fancy name I give to a method that basically combines curved surfaces with deformation of the landscape. As you tesselate further and further, the deformation becomes less and less. Here is a description of the algorithm with more detail: From the heightmap points, I can generate biquadratic Bezier patches. Biquadratics are quicker to tesselate than bicubics, and also require less control points. However, I personally don't use Bezier patches, but rather the curved triangles I described in previous tutorials. This is because of being able to switch LOD easily as I described in those tutorials. If an edge of a triangle doesn't have enough subdivisions, you can split the triangle (with n subdivisions on each side) along that edge into two triangles (each with n subdivisions on each side), and as a result that one edge will have twice as many subdivisions as before. With rectangular patches you cannot do this, because you can't split a rectangle (with n subdivisions on each side) into other rectangles (each with n subdivisions on each side) and only increase the number of subdivisions along one edge of it. So, anyway, you have your bi-quadratic patches, whether they be quadrangular or triangular. These were obtained from a pretty sparse heightmap -- the points might have been located 200 "meters" away from each other. If you just draw these patches as they are, you will get smooth rolling hills... which are nice, but aren't that realistic if they're everywhere. Instead, it would be nice to introduce some deformations in the landscape. They could be large deformations when the tesselation is only beginning, but as we get a higher and heigher level of detail the deformations will be smaller and smaller. The deformations I refer to are simply adding or subtracting some values from the actual height, each time subtracting smaller and smaller. Instead of curved surfaces, in fact, you could generate progressive maps like we described before, only algorithmically, creating the Tip vertices yourself based on random seeded deformations. Actually, you can have the following parameters for the landscape:
The functions and seeds, like the heightmap, can be changed on a per-area basis. The individual areas are generated, but you can control what kinds of areas are where. If you have the exact same height, functions and seeds in two areas, they will look the same. But the chance of that is small, and you control that chance... you build the map. Each of these values is smoothly blended between the points of the map that you specify. Note that these things are all landscape data, and must be specified. When you have a multiplayer game and several people are in the same place, you want them to see the same landscape. If you use this approach to half-specify, half-generate landscape, you can generate very, very large maps, that will have a lot of detail, and where anyone in any place will see the same thing. You can use other such algorithms or modify this one, to produce limitless (in theory) maps, but for those maps you probably won't specify the heightmaps and other things yourself -- just leave it up to the landscape generator. |
Texturing
 |
|
Now that we have talked about algorithms involving landscape shape, we will move
on to other things. One of these is texturing the landscape. Sofar, we have been
thinking in terms of polygons and triangles, and used one texture (or no
texture) for the whole landscape. Let's consider the subject of texturing. First of all, you have a basic problem. Let's say you had a texture of grass, and you wanted to use it on the landscape. The texture itself will maybe fit across one or two heightmap cells. If you just tiled it, you could get okay results, but the tiling would be noticeable by people moving over the terrain. You could try to vary lighting hide this tiling effect, which we will talk about later. You can also use various noise functions and overlay them over close-up textures, producing interesting effects (see links). Now let's think of another scenario. Suppose you had a few textures: mud, sand, dirt and grass. Now, from these four textures you can generate transition textures. Mud<->Sand, Sand<->Dirt, Dirt<->Grass. I'd recommend making a few transition textures for each <->. You can prepare the transition textures before you render the landscape, and you can do it as follows: First you use your artistic talent to make a blending mask. You can have several different blending masks that you can use for textures. It's usually good that all the transition textures can match up to each other from left or right, so you can mix and match them in any order, and not just repeat the same thing over and over. Here's how you would use a blending mask to combine, say, the dirt and the grass textures:  If you did this with all three blending masks, you would create three transition textures, and you could mix and match them in random order as you draw your landscape. (Remember that when I say "random," it means in most cases not truly random but based on a certain seed. So, again, if you have several people in the same place on a network game they would see the same landscape!) Now, you have the various textures and transitions between them. How do you determine where to use which texture? Well, some you can determine based on height. For example, down below you'd have mud, which would change to sand as you moved up, then dirt, and finally grass. Maybe when you get very high on some mountains you would have snow. However, some textures, like dirt and grass, you would probably want to change not based on height but rather slope. If a slope is above some threshhold, you'd use rock/dirt for that polygon/triangle. If it's below, you'd use grass. When you're tesselating meshes into smaller pieces, using whatever method, you should keep track of the slope of each piece to determine its texture. You can use these methods, but I'd also suggest doing at least some kind of texture specifying yourself. If you're making an engine, along with the heightmap it could also accept some sort of map containing the conditions for the texturing. More grass here... more dirt there... more randomness in this area... etc. So you can make dirt roads and all kinds of other stuff. After some experimentation with these techniques ,you should be able to create rather realistic-looking landscape features by using textures to your advantage. |
Lighting & Fogging
 |
|
When I talk here about lighting, I really mean casting shadows on the landscape.
Normally you could code a landscape engine without large-scale, and it would
look pretty good. When the "sun" is directly overhead, for example, everything
is lit. But the shadows do add a certain depth to the scene. Also, you can light
some terrain based on its slope, which is not the real way to peform lighting
but does give a certain feel of "dark places" on the landscape. Moreover, some shading can be used to simulate small-scale shadows of rough-looking terrain. You can produce terrain that looks rough without actually having to tesselate it and light it. You can just overlay a lightmap on a texture and produce little subtle holes in the ground, waves in the sand, etc. This is usually much faster than tesselating a texture and figuring out lighting based on slope. You can achieve some interesting effects using noise functions like Perlin noise (see the links). Mostly, though, lighting is still static and precalculated before the map is rendered., because generally computers still aren't fast enough to do it on the fly. A shadow-map for the whole landscape could be computed from the heightmap and the angle of the "sun's" rays. It works like this:  We want to light only the parts of the landscape that can receive light as it comes from some angle. In theory, we can trace rays from each point in the landscape back towards the sun, and if we hit anything, that point we were tracing from is in shadow. Of course it's too much computation to do this for every point in the landscape, but you can do it for every point in the heightmap. As for fog, it is used as a cheap atmospheric effect, and doubles for hiding terrain inifinitely away. While it is true that "natural" fogging does occur for very far-away mountains and such, that kind of fog should be limited to very far away objects. Closer than that, fog should be used judiciously as a mist in valleys, for example. Landscape is one of those things that can potentially be visible for great distances. Unlike indoor shooters, stuff like flight simulators or racing games need to find some way to handle this. Early games used to just cut off the scenery after a certain point, so it was noticeable when new scenery popped onto the screen. Nowadays most programs use fog to fade out into nothingness. If you're making flight simulators or something similar, consider not using fog exclusively for hiding far away terrain. Instead, switch from drawing polygon strips to something even less detailed: a horizon plane. Use fog with the same color as the horizon plane to fade the terrain into it. Or perhaps you could try mapping a texture onto that horizon plane. In any case, remember to draw the horizon plane first, and disable zbuffer writing when you draw it on hardware, so it doesn't overlap anything. (Next time I'll talk about, among other things, making the horizon plane work with the sky.) |
Conclusion
 |
|
We've begun to cover a very interesting topic -- landscapes. Landscapes are one
of my favorite types of scenery, and have their own class of rendering
techniques. I can see a lot of other people like them too :) But, of course, this is a big topic. When I said I'd write about it, I realized I wouldn't be able to cover it in one issue of my column. Next time we'll talk about many more things that enhance simple landscape rendering. Among these will be: drawing the sky, drawing objects on the terrain, some attempts at tree-drawing techniques, as well as modeling realistic water. Besides rendering, there are also issues like collision with the landscape to be dealt with. I hope you enjoyed this time. As always, if you're interested, try and implement what I'm talking about, because once you start getting it, it becomes quite fun! Some of you have suggested I provide some practical code examples as I write. How do you think I did this time? ;-) Write to me and tell. And stay tuned until next time! :-) |
Links and Acknowledgements
 |
|
The pictures in Figure 4 of this issue have some suspicious similarities to a
tutorial by Alex Champandard. I hope he doesn't mind... I couldn't get a nice
blending map from anywhere on short notice. For more info on quadtrees go read Continuous LOD Meshing Using Adaptive Quadtrees, by Thatcher Ulrich Here's an article on Real-Time Dynamic Level of Detail Terrain Rendering with ROAM, by Bryan Turner. (BTW, it's dedicated to the memory of Seumas McNally.) Want to learn about Perlin noise to spice up your terrain? Take a look at Ken Perlin's own page. All this talk about landscape makes me want to go out and enjoy nature. I suggest you do the same :-) |