|
3D Geometry Primer: Chapter 1 - Issue 08 - Point Arithmetic by (02 October 2000) |
Return to The Archives |
Point Arithmetic
 |
|
The last issues of chapter 1 are going to handle Point Arithmetic (not
pointer arithmetic! that's something completely different). Thanks to the
place vectors we introduced last week, it becomes quite easy to work with
points in your software: you simply do all calculations on the place vectors,
the result is a new place vector which represents your resulting point. But then you ask: "If you simply do the point arithmetic on the place *vectors*, then why bother about *point* arithmetic? Isn't it the same as vector arithmetic?" Yes and No. You indeed *use* vector arithmetic to perform your point arithmetic, but there's one major problem: the influence of the origin! The real world doesn't have an origin (like we discussed last week), but your model - that uses place vectors - does! So, if you want your model to be a good representation of reality, you have to make sure that it works independent of it. This is becoming quite confusing. Maybe an example will help... |
(I) Problem ...
 |
Take 2 points P and Q in the real world. OK, you have them? Now add those
points P and Q together. What is P + Q? Can you figure it out? No, probably
not. Why? It's hard to explain, but this sum seems to mean nothing. We'll try it once more. Take a sheet of paper and draw those points P and Q on it. Also, choose a point O as origin. Now you can pull the place vectors of P and Q: OP, and OQ. You get the following picture: 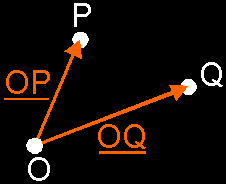 Now try to add those points P and Q again. What is P + Q? Your instinct will try to add those points by adding both place vectors together. It will say: If OP is the place vector of P, and OQ is the one of Q, then the place vector of (P + Q) is (OP + OQ). Congratulations, you have a fast instinct. But is your instinct correct? Unfortunately not. Why? Choose another origin O' and draw place vectors O'P and O'Q to P and Q. Now try to add P and Q once more. If you use the same trick, you will get a different result. 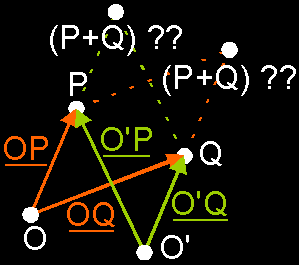 ...And that is something that can not be! You can't have 2 different results for a problem that asks for only 1 sollution. This is how its proven that you cannot do P + Q Then, what *can* we do with points? Well, ... |
(II) Translation: Sum Of A Point And Free Vector: P + V
 |
|
The first thing that we're going to examine is the addition of a free vector
to a point. How can it be defined and interpreted? Definition: The addition of a point P and a free vector V results back in a point (P + V). That point (P + V) is given by the ending point of the representative of V in P. Wow! Let's say this i.e.: take that free vector V, put it with its tail in the point P, and your resulting point will be the head of vector V.  But how do we put this in our computer? Well, you already know that you use a place vector OP to store your point P: that place vector contains the coordinates of P. So, all you have to do is to replace P by its place vector OP. In that way, you really calculate the sum OP + V, which is a sum of 2 vectors and you already know how to do this. As result of this sum, you will get - suprise, suprise - a new vector. And that one is exactly the place vector of (P + V): it will contain the coordinates of the resulting point. 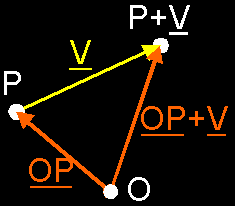 In plain English, please! OK, you use coordinates to store your point P, don't you? Yes, let's say these coordinates are P(p1, p2, p3). I hope you still remember of last week that these coordinates are actually the component values of the place vector OP of point P: The place vector of P(p1, p2, p3) is OP(p1, p2, p3). Also, let us assume that the component values of vector V (the one we want to add to P) are V(v1, v2, v3). Now, to add V to P, you simply add all component values together: P(p1, p2, p3) + V(v1, v2, v3) = (P + V)(p1+v1, p2+v2, p3+v3). 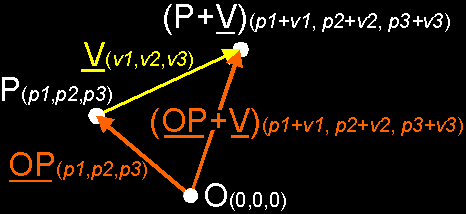 This result depends on the origin? No, where do you see an origin in the definition? Nowhere! OK, great... If you don't believe, try to draw several situations on paper and feel the magic. interpretation: You can see all this as moving a point P in a certain direction and sense, and over a certain distance to a "new" point (P + V). That's why it's called a translation: you translate P to (P + V). The vector V is the "prescription" of this translation: you move P v1 units in the x-direction, v2 units in the y- and v3 units in the z-direction. So, if you need to move one or more points in a certain direction, you simply construct a free vector that prescribes this translation, and you add this vector to all points needed to be moved. An example: we want to move points P(1,2,3) and Q(2,4,0) 3 units along the z-axis. Maybe because it are 2 little spaceships traveling with the same speed in that direction. So, we prepare a vector V that contains this translation: V(0,0,3). And now, we apply this vector on P and Q: P + V = (P+V)(1,2,6) and Q + V = (Q+V)(2,4,3). 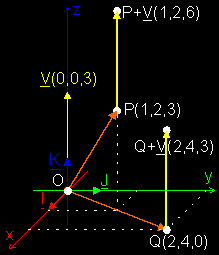 Why is this *cool*? Well, to move objects of course, but one of the other common things you need to do in a rendering pipeline, is to move the camera to the origin ... Normally the camera doesn't stay in the origin; no, you want to walk around in your world. So, you store its current position of the camera C in a place vector OC(c1,c2,c3). OK, now we know where it is, we want to render our world. *But*, to do this, we need our camera back in the origin without changing the view! What you have to do, is to translate ALL points (including the camera) in the *same* way, so that the relative position of all points remain the same, and the camera is in the origin. What translation do we need? If you look at the picture, you can see that you need to translate all points over –OC. If you do that, you will see that the camera will be back in the origin, and that the relative position of all points will remain the same. 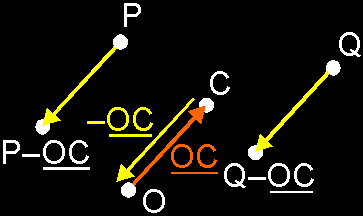 REMEMBER: To add a free vector to a point, add the free vector to the place vector of that point. |
(III) Difference Of 2 Points: Q – P
 |
This is very analogue with the previous one. Watch it!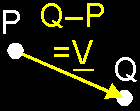 Definition: If you subtract one point P from another point Q, you get a free vector V as result: the one that fits between P and Q and with it sense from P to Q. So, Q – P = V. This is all very logic. Why? If you shuffle the symbols a little bit (move P to the right side), then you can rewrite this as: Q = P + V, or P + V = Q. Do you see the similarity with paragraph (ii)? An addition of a point P and a free vector V that results in a point Q. I always use this "shuffling" to know the sense of the vector (Q – P). Does the vector point from P to Q, or from Q to P? It's easier to solve this problem if you rewrite is as P + ... = Q. Now, it's easy to see that you have to fill in a vector that points from P to Q How to put this in your computer? As with the addition, you simply replace all points by their place vectors. In this way you actually make the difference of 2 place vectors instead of 2 points: V = OQ – OP. And of course, you get a vector as result then ... Check out issue 02 paragraph (iv) to convince yourself this has the same result. Also, try using another origin with the same points. You will see that the result is independent of the origin! Which is of course *very* important :) 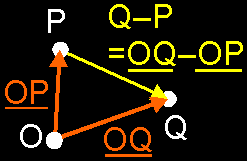 In plain English: simply subtract the coordinates, and you get the vector inbetween the points: Q(q1,q2,q3) – P(p1,p2,p3) = PQ(q1–p1, q2–p2, q3–p3) An example: We have 2 points P(1,2,3) and Q(2,4,0), the same ones of last example. Now, we want to find the vector V inbetween P and Q (maybe we want to translate P to Q ...). So, what we do is to subtract P from Q: V = Q – P = V(2–1, 4–2, 0–3) = V(1,2,–3). 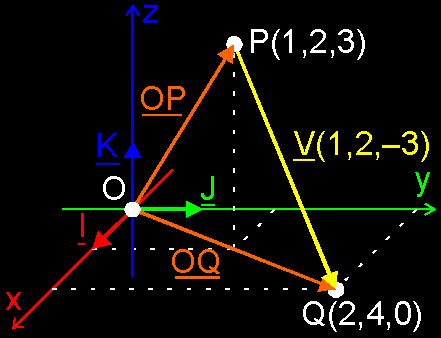 You might want to check this by translating P by V now: what is P + V? P(1,2,3) + V(1,2,–3) = (1+1, 2+2, 3–3) = (2,4,0). And this is exactly the same as Q(2,4,0), what we've expected. REMEMBER: If you make the difference of 2 points, you get the free vector in between. Next week we're going to add 1 more operation with points: barycentric combinations. It's a way to extract out of n original points P[0], P[1], ... , P[n-1], a resulting point Q in a way independent on the origin.  It's much like linear combinations of vectors (in fact, you will *do* a linear combination of the place vectors OP[0], ... , OP[n-1]), except that there will be a condition to make it independent of the origin. There're many possible Q's for each set of P's, depending on which combination of the P's you take. I wanted to add this here but it would take up too much space, so you will get it next week. Then, you will know the 3 operations you can do with points: point + vector, point – point, barycentric combinations. It doesn't seem like much, but it really covers all operations you will need. OK, I will see you next week for the barycentric combinations. Regards, the Bramz "He never is alone that is accompanied with noble thoughts." - Fletcher |