Hopefully you know what normals are. Here's a quick diagram to illustrate a normal
in 2D. As you can see, they're directions perpendicular to the original 'surface' (our line),
and extend on both sides (forming 90 degree angles).
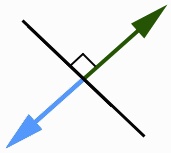
The same applies in 3-space such that the normals are orthogonal to the original 'line'.
Imagine for example the line as an infinite plane in 3D. The normal is a vector that is orthogonal
to that plane. They're used for a lot of things in 3D calculations such as backface culling (by checking
what direction a polygon is facing, in other words which way the polygon's normal is pointing). So that's nice, but...
Say you want to work with lighting and shading some of your objects. Check out the following (attempt at a) picture:
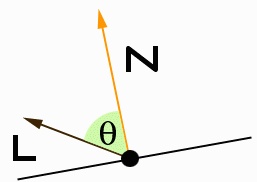
In many lighting computations (there are many local reflection models to choose from, so I won't mention any in particular), one would use the angle between the normal and the light vector
to determine how much light is being reflected (as well as mirror angles, view angles, etc -- this depends on what kind of lighting you're doing), thus
labelling the surface with a certain 'brightness'. This document isn't about lighting, so I won't get into
much about the properties of light or how things reflect, but you may have gathered that using face normals (the normal of a polygon 'face'), we can only get a particular
'brightness' for an entire polygon. That would be nice if we only wanted to do flat shading, but that's
painfully boring for most games and demos. Our goal is to find a normal for EACH vertex that we can use.
This would let us, for example, interpolate the 'brightness' across the surface for
use with techniques like gouraud shading, or even interpolate the normal itself for use with phong shading.
So how do we get these magical normals? Because normals don't exactly exist at the vertices, I believe some
people call them vertex psuedo-normals. We can get a pretty good idea of what they should be by
simply averaging the surrounding face normals. That is to say -- the normals of the polygons that share
the particular vertex whose psuedo-normal we are trying to compute. Not too bad, eh? This works
ok for typical objects like spheres, torii, and so on -- as long as the polygon arrangements offer a decent representation
of the actual object they're representing, this method should do fine. So now like the light angle
picture above, you can use the vertex normal instead of the face normal to calculate the brightness
at any particular vertex. Hopefully you see why that is a good thing. Below is some general psuedo-code.
Psuedo-Code:
// Calculating vertex normals using a vertex list and polygon faces (vertex indices);
loop through your vertex list {
clear this_vertex_normal; // initialized to [0,0,0]
loop through your face lists {
for each face vertex, check if its
the same as the vertex as in our
current outer vertex loop.
If it is, {
this_vertex_normal += this_face.normal;
}
}
this_vertex_normal.Normalize();
}
|
|




