|
Introduction To Octrees by (13 April 1999) |
Return to The Archives |
Introduction
 |
|
Hidden surface removal is among the biggest problems
when writing a 3D engine. I struggled with it since the very beginning of writing 3D engines and still have no satisfactory solution to it. The ideal visibility detection scheme would allow unlimited data, extremely dynamic worlds and would have zero overdraw. The first 3d engine which implements these three demands still has to be written. The Z buffer for example allows dynamical worlds and even crossing faces, but it suffers from immense overdraw. The BSP-tree on the other hand, if well implemented, has no overdraw at all but needs that much pre-processing that dynamical worlds are a definite nono. It wasn't until recently i first heard of the octree, and I must admit i was struck by it's simplicity. I never actually implemented this structure and therefore I will present no pseudo code at all. This explanation is merely an attempt to make it more clear to people who have never heard of it. Besides, if you really understand the structure, then implementation is a piece of cake. |
The Octree Structure
 |
Our virtual world or level is actually nothing more then a soup of
polygons. Some of you people might have thrown in a couple of curves and voxels but most
of it will be polygons. Here it is: Fig 1. Our little level. In the picture I just built a simple level containing no more than 250 polys. Now imagine a cube surrounding the world like in the next image: 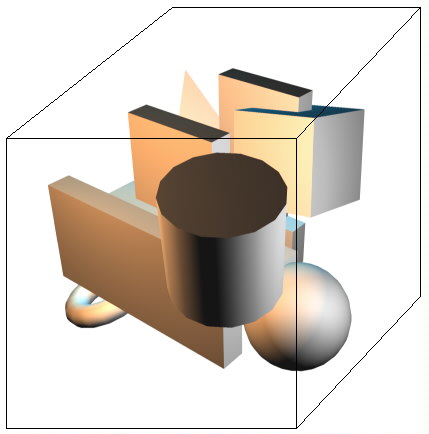 Fig. 2. Our little level surrounded by a cube. Now it isn't hard to see that this cube can be divided into eight smaller cubes, hence the name octree. Take a look at this picture:  Fig 3. Our little level with the surrounding cube subdivided. Call the larger cube the parent and the smaller cubes the children. On their turn subdivide each children into eight smaller cubes, and you will notice we are creating a tree where each node has eight children. There is still one little problem left. When should we stop dividing cubes into smaller ones? There are two possible solutions. The first one is to stop when a cube has some size smaller then a fixed number. The second one is more common. You might have noticed that every child has less polygons then it's parent. The trick is to stop subdividing when the number of polygons in a cube is smaller then some fixed number. |
Creating The Octree
 |
|
Trees are recursion, recursion is trees. It is as simple as that.
If you have a correct definition of you cubeNode it is very easy to create an octree
recursively. First of all you check all polygons against the boundarys of the cube. This
is very simple cause these boundaries are all axis aligned. This means that the cube has
six plane equations, which are: Where Q is the position of one corner of the cube. This are very easy equations and the all parent polygons can very easily be checked against them. It could occur that a polygon crosses a cube boundary. Again two possible solution are at hand. First of all we could clip the polygon against the cube, which is simple, because of the axis aligned boundarys. On the other hand we could put the polygon in all cubes it is in. This means that some cubes can contain the same polygons. In order to prevent us from drawing one poly more than one time we should have a flag on each polygon which will be set if the poly is drawn for the first time. The implementation of an octree is very straight forward. I haven't done it myself yet, but I will soon. It is all matter of recursion. In order to construct a tree, the first thing you should think of is recursion. Whether we are talking about binary trees, quad trees or octrees, it doesnt matter, just build the darn thing recursively. So have a class definition of one cubeNode and put the creation of the tree in it's constructor. In this constructor you will call the constructor itself for smaller cubes. |
The Purpose Of The Octree
 |
|
An octree is actually nothing more then a data structure. It
can be used for very different things. It is not only handy for visibility detection but
also for collision detection, realtime shadows and many more things. The most important
thing to understand about octrees is that if a parent is not important then it's children
aren't either. Let's makes this a little bit more clear with an example. We will do this in 2d, which therefore resembles a quadtree, but with some imagination it can very easily be extended to 3d. Here we test the cubes (squares) against the viewing frustrum. Take a look at the next picture: 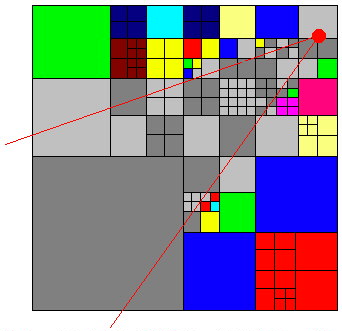 Fig 4. An octree from the top and a viewing frustrum. In this picture a colored square that has one color was dumped without checking itís children. As you can see some squares had to be checked all the way to the final node, but some large squares could be dumped at once. The colored squares are the ones that are outside the viewing frustrum and the greyscale ones are the one inside the viewing frustrum. As you can see this is actually a worst case scenario because the viewing frustrum crosses the middle of the surrounding square and therefore all the four children have to be checked. You could also apply the octree to many other things. Collision detection for example. Just check in which cube your bounding sphere or box is and you will only have to check against those faces. There are many more examples. |
Conclusion
 |
|
There is already a lot written about octrees. I tried to
give my view on them in the hope somebody might read this. As you can see octrees are
way easier to implement than BSP-trees (although some disagree) while offering a better
structure. The main point about an octrees is that when a parent is discarded so are
it's children. Actually that is all there is to it. Code clean, play Goldeneye and go vegetarian. Jaap Suter a.k.a ......... |
|
|