|
Interpolating Normals For Ray-Tracing Question submitted by (21 September 2001)  |
Return to The Archives |
 |
 |
|
| I have a problem about raytracing. When my raytracer found an intersection with a polygon, it always use the normal of polygon to compute shade. This give to the image an faceted look. I read that to avoid this problem is necessary to use interpolated vertex normals. I have already computed the vertex normals, but it's are only in the VERTEXES of poly. How I can compute (interpolate) it for the intersection point, in order to obtain smooth phong shading? | ||
 |
 |
 |
 |
||
To solve the problem, you really need to do two interpolations. Consider figure
1 (note that I'm using color for interpolation, rather than normals, though the
two are interchangable):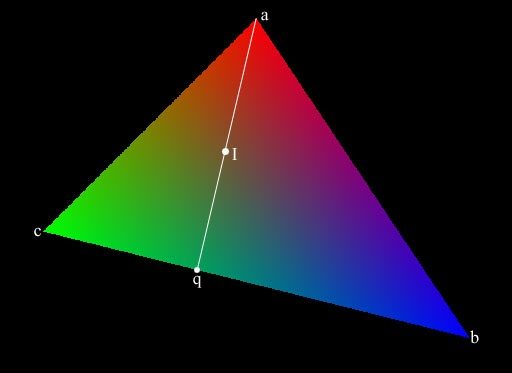 In figure 1 the polygon [a, b, c] is intersected with a ray at point I. In order to find the color at I, we'll need to interpolate twice. First along the [b, c] edge to find the color at point q, and then along the [q, a] edge to find the color at I. Let's cover this in more detail... The first step is to find q. In our diagram, q lies on the edge [b, c]. The choice to use [b, c] is not arbitrary. In order to maintain accuracy, we need to find the vertex that is farthest from I. We then use the other two points to define an edge that will be used for the first interpolation. If we don't do this, we might find ourselves working with very poor accuracy as the rays intersect our trangle near the vertices. Now that we've found the edge we want to use for interpolation, we project I onto that edge to find q. In my case, I just created an edge plane and performed another ray/plane intersection. This can also be done by calculating a base, but I think the difference in the amount of effort between the two options ends up being about equal. Once we've located q, we simply interpolate the color from b->c to find the color at q. This gives us a color and a location for q. We also have a color and location for point a. With one more interpolation (between [q, a]) we can find the color for I. I wrote a mini test ray tracer to verify the results, and the above image is a result of that test code. The code for the interpolation is as follows:
 Response provided by Paul Nettle |
|||
 |
 |
|
This article was originally an entry in flipCode's Ask Midnight, a Question and Answer column with Paul Nettle that's no longer active. |