flipcode - Faster Vector Math Using Templates

Faster Vector Math Using Templates
by (22 March 2001)

Introduction

In the quest for knowledge we must try all kinds of new ideas. Not too long ago I came across an interesting article written by Jim Blinn. (He is one of the real pioneers of computer graphics. He currently works for Microsoft as a researcher. Jim invented bump mapping, the new specular formula being used in D3D, and so on.) He was talking about faster ways of implementing vector math using templates and observed that the most common method of implementing a vector class is wasteful with the stack and registers. The goal of this article is to demonstrate these concepts and create our own implementation.

You are about to embark upon one of the strangest articles you have ever read on C++. So if you are… let’s say… uncomfortable with the language, you may experience some vomiting sensations. But not to worry, after reading it a couple of times I am sure it will become clear. I will try to explain how Jim is right and how the Microsoft compiler can’t handle the truth. Well, not so much the truth as the templates, but you get the picture.

Defining the problem

Mind you, there are many ways to do a vector class, but the most typical case is shown in Listing 1. Let’s start analyzing this code. As you can see, the operator + function returns a vector3d object. Of course, the return value is placed in a anonymous temporary value on the stack. Then, the operator = function (even if it was generated by the compiler like in our example) is used to move the result data from the anonymous object on the stack to the final destination. Of course, under the right circumstances, the optimizer can help out substantially on this type of problem.


struct vector3d
{
    float X, Y, Z;
 
    inline vector3d( void ) {}
    inline vector3d( const float x, const float y, const float z )
    { X = x; Y = y; Z = z; }

    inline vector3d operator + ( const vector3d& A ) const
    { return vector3d( X + A.X, Y + A.Y, Z + A.Z ); }

    inline vector3d operator + ( const float A ) const
    { return vector3d( X + A, Y + A, Z + A ); }

    inline float Dot( const vector3d& A ) const
    { return A.X*X + A.Y*Y + A.Z*Z; }
};

// Listing 1

Assume we have an expression like this: vA = vB + vC + vD. How many vector3ds are going to end up in the stack? Let’s walk through step by step. The first thing that happens is that vB + vC gets executed, so that is where our first temp (call it temp1) is created. Then temp1 + vD is going to execute. This will create the temp2 object. Finally, temp2 will be copied to vA. What a waste, huh? We would much prefer that the compiler not generate any temps and refrain from reading and writing from memory unnecessarily. Listing 2a shows some pseudo assembly that demonstrates that.


Mov  eax, vB.X
Mov  ebx, vB.Y
Mov  ecx, vB.Z

Addf eax, vC.X
Addf ebx, vC.Y
Addf ecx, vC.Z

Addf eax, vD.X
Addf ebx, vD.Y
Addf ecx, vD.Z 

Mov  vA.X, eax
Mov  vA.Y, ebx
Mov  vA.Z, ecx


Mov  eax,  vB.X
Addf eax,  vC.X 
Addf eax,  vD.X 
Mov  vA.X, eax

Mov  eax,  vB.Y
Addf eax,  vC.Y
Addf eax,  vD.Y
Mov  vA.Y, eax

Mov  eax,  vB.Z
Addf eax,  vC.Z
Addf eax,  vD.Z
Mov  vA.Z, eax

Listing 2a

Listing 2b

But even Listing 2a is still wasteful because it uses more registers than it needs. We can improve that by using Listing 2b. As you can see only one register is used. The important concept is not really that we used only one register, but that we have done all the operations in each of the dimensions independently. The reason why this concept is so important is that when we have an expression that requires intermediate results, the compiler has a much better chance to keep everything in registers. For instance, let’s say that we have an expression that looks something like this: vA = (vB + vC) + (vD + vE). The compiler will first do vB + vC which will generate temp1, then vD + vE and create temp2 then it will add both temps (temp1 + temp2) which will generate temp3. Finally, temp3 is assigned to vA. The problem is that temp1 and temp2 exist at the same time. That means that we have 6 floats in our hands if we do all the dimensions at the same time. But if we do one dimension at a time then we only have 2 floats to deal with. The best part of this is that the method scales up very gracefully. For instance, what will happen if instead of having a vector3d we had a vector16d? If we do one dimension at a time we still have only 2 floats using the method in listing 2b. But if we do it like in listing 2a we will have 32 floats. Guess which method is more likely to use the registers efficiently.

Defining the tool to solve the problem

Now that we have seen how painful it can be using the common implementation, we must improve upon it somehow. The first thing that we will need is to define a tool that will allow us to change the situation. I’ve chosen C++ and templates to solve the problem. Templates still are an area of exploration. In 1994 Erwin Unruh presented to the C++ Standards Committee a template program that generated prime numbers. The program didn’t compile, but in its error messages it displayed the prime numbers. This created a new way of thinking about templates.

Templates are one of those kinds of things that people either love or hate. But like most things, it is what you make of it.

Defining the solution

So how to go about solving the problem? Currently, each sub expression is completely solved for all three components (x, y, and z) before moving on. We are going to change the order a bit. Without regard to the complexity of the expression, we want to completely solve for just the x component, then for y, and then for z. (Within our studio, we call this “rotating the problem 90 degrees”.) Let’s first start with a simple formula: vA = vB + vC. The final C++ code has to expand to something like this:


vA.X = vB.X + vC.X;
vA.Y = vB.Y + vC.Y;
vA.Z = vB.Z + vC.Z;

Let’s first build a structure that will take our original formula and break it into a set of expressions. For that we are going to have to create a new class. This class is going to be in charge of holding one part of the formula. In this example there is only one part, specifically vB + vC, since the expression contains only 2 vectors. Actually, all the operations that we are going to deal with involve 2 or less vectors. We will call the new class vecexp_2. This class can be found in Listing 3. There are some other changes that we need to make. The vector3d class needs to be able to get each dimension in a generic way. What better way than an array of floats (see Listing 3)? Next, we are going to create an operator + function outside the class. Later on, it will become useful to have done it this way. Finally, if you keep looking at Listing 3, you will notice that we have a structure called sum. This looks a bit like overkill for what we are trying to do, but again it will make sense later on. Take your time to figure out how all this works.


struct vector3d
{
    float V[3];
    inline float Evaluate( const int I ) const { return V[I]; }
    inline const vector3d& operator = ( const vecexp_2& Exp )
    {
        V[0] = Exp.Evaluate( 0 );
        V[1] = Exp.Evaluate( 1 );
        V[2] = Exp.Evaluate( 2 );
        return *this;
    }
};

struct sum
{
    static inline float Evaluate( const int I, const vector3d& Va, 
                                               const vector3d& Vb )
    {
        return Va.Evaluate( I ) + Vb.Evaluate( I );
    }
};
 

class vecexp_2
{
    const vector3d& V1;
    const vector3d& V2;
public:
     inline vecexp_2( const vector3d& Va, const vector3d& Vb ) 
      : V1( Va ), V2( Vb ) {}
     inline const float Evaluate( const int I ) const
     { return sum::Evaluate( I, V1, V2 ); }
};

 
vecexp_2 inline operator + ( const vector3d& Va, const vector3d& Vb )
{
    return vecexp_2( Va, Vb );
}

// Listing 3

Let’s now follow what happens to our original expression vA = vB + vC. First, function operator + will be called with vB and vC as references and will create a vecexp_2. Note how we call the constructor and pass both references. Those references will be stored within the vecexp_2 class when the constructor executes. After the vecexp_2 is constructed, it is passed to the vector3d function operator = because we are assigning the constructed vecexp_2 to vector3d vA. This operator = in turn calls the vecexp_2 function Evaluate for each of the dimensions. This results in the sum::Evaluate function being called. Here we call each of the vector3d::Evaluate functions and finally the results are added and returned.

All this looks like overkill, but it is a stepping stone. It may seem that we just added tons more overhead to get the same thing as before. But actually, to everyone’s surprise, if the code is compiled in release mode, it will run a bit faster than the original.

What happened? Well for one thing, we added tons of const’s and inlines everywhere. This caused the optimizer to inline everything, and it creates the result that we wanted in Listing 2b. Crazy isn’t it? Well, get ready for a lot more craziness. The problem with the current program is that it’s unable to handle longer expressions. To solve problems with longer expressions we need to use templates. Where do we need templates? Everywhere!

Let’s try to solve a more complex problem: vA = vB + vC + vD. Our code right now will pick up vB + vC and create a vecexp_2. Note that now we could write one more function to solve this particular problem. The prototype of that function would look like inline operator + ( const vecexp& Exp, const vector3d& B ). The problem of heading this direction is that we would need a new expression class. This would cascade and require changes all over the place forcing us to add way too much code to make it practical. Not to worry, here is where we introduce the templates to solve all these problems in one shot. Listing 4 has the new source code.


struct vector3d
{
    float V[3];
    inline float Evaluate( const int I ) const { return V[I]; }

    template< class ta >
    inline const vector3d& operator = ( const ta& Exp )
    {
        V[0] = Exp.Evaluate( 0 );
        V[1] = Exp.Evaluate( 1 );
        V[2] = Exp.Evaluate( 2 );
    }
};

 
struct sum
{
    template< class ta, class tb >
    static inline float Evaluate( const int I, const ta& A, const tb& B )
    { return A.Evaluate( I ) + B.Evaluate( I ); }
};

 

template< class ta_a, class ta_b, class ta_eval >
class vecexp_2
{
   const ta_a   Arg1;
   const ta_b   Arg2;

public:
    inline vecexp_2( const ta_a& A1, const ta_b& A2 ) 
     : Arg1( A1 ), Arg2( A2 ) {}
    inline const float Evaluate ( const int I ) const
    { return ta_eval::Evaluate( I, Arg1, Arg2 ); }
};
 

template< class ta, class tb > inline
vecexp_2< ta, tb, sum > 
inline operator + ( const ta& A, const tb& B )
{
    return vecexp_2< const ta, const tb, sum >( A, B );
}

// Listing 4

Let’s first focus on the vecexp_2. Note how it takes 3 classes in the template argument, the two operands and the operator. This will allow any operator that uses two operands to use its functionality, which produces the virtual like functionality. The only requirement is that you have in your operator a function called Evaluate(int I). For this article we are only going to do the sum, but you’ll see how adding the rest of the operators are trivial. In the structure sum you will notice that it also has the same concept for the operands. We only have two types of operands so far, vecexp_2 and vector3d. Note that other classes that are not vector related could be passed to any of our generic template classes by mistake, but we will address that problem later. The other big change that has been added is in the function operator +. Now it takes two objects of any kind and it builds a vecexp_2. The syntax for all of this is a bit heavy so it may take a bit to get familiar with all this, so take your time.

Congratulations if you made it this far! Now you have the basic concepts about templatized math. If you don’t understand what we just did, I don’t blame you. Just take it easy and try understanding one item at a time. Once it’s in your head, try to see how the whole thing works.


template< class ta_a >
class vecarg
{
    const ta_a& Argv;
public:
    inline vecarg( const ta_a& A ) : Argv( A ) {}
    inline const float Evaluate( const int i ) const 
    { return Argv.Evaluate( i ); }
};

 
template<> 
class vecarg< const float >
{
    const ta_a& Argv;
public:
    inline vecarg( const ta_a& A ) : Argv( A ) {}
    inline const float Evaluate( const int i ) const { return Argv; }
};
 

template<> 
class vecarg< const int >
{
    const ta_a& Argv;
public:
    inline vecarg( const ta_a& A ) : Argv( A ) {}
    inline const float Evaluate( const int i ) const { return (float)Argv; }
};

 
template< class ta_a, class ta_b, class ta_eval >
class vecexp_2
{
    const vecarg<ta_a>   Arg1;
    const vecarg<ta_b>   Arg2;

 
public:
    inline vecexp_2( const ta_a& A1, const ta_b& A2 )
     : Arg1( A1 ), Arg2( A2 ) {}
    inline const float Evaluate ( const int I ) const
    { return ta_eval::Evaluate( i, Arg1, Arg2 ); }
};

// Listing 5

Okay, now we can solve any type of expression that involves additions with other vectors. Fantastic! Let’s push it a bit more and try to do it with two types, vectors and numbers. That way we can write this other interesting expression: vA = vB + 5 + (vC + vB). The first thing to consider is that the operator + will take any type. That of course includes integers, and floating point numbers, which is what we want. But the problem is that an integer doesn’t have a member function called Evaluate. This will cause our whole system to fail miserably. Well, don’t worry—it’s not that bad. We just need to add another class called vecarg. We don’t want to add complexity to the operators since we have a few more operators to write, such as *, -, /, etc. We would like to add the complexity in the vecexp_2. You can look in Listing 5 to see what the new changes to this class have been. As you see, vecexp_2 is wrapping all its types with the class vecarg. The vecarg class creates a generic template for all types. You will notice that inside the class it also has a member function called Evaluate. Again, this forces any type to have that function. This is a good thing since this class will solve two problems. The generic version of it still assumes that the basic type has a function called Evaluate. We want to do that because it will allow us to create a compile time error for any unfriendly types such our famous banana class. The second thing that it solves is that it creates a template from which we can create particular instances. Look at the other class in Listing 5. Now we have an int and a float argument with the function Evaluate. This will force the compiler to use these classes instead of the generic vecarg version.

Defining the features

Basically we are about to finish the whole framework. We just need to clean it up and add a few missing pieces. One detail I want to add, because I think it is worth it, is the ability to have a multidimensional vector class. That means that we can have a vector2d or vector4d or whatever else we want. Most game programmers will find useful the ability to use 2D, 3D, and 4D vectors. Some of you may even be using 6D vectors for visibility stuff. I also added another feature just for fun, this feature will allow us to say vA.X rather than vA.V[0] because an array like that is very unfriendly. Also, you may want 2 different names for such things as UV vectors, versus XY vectors. Furthermore, let’s clean up the entire thing and put it in a namespace to make sure we never collide with any other function name. Up to the challenge? Don’t worry, this part is simple…


namespace vector
{
//////////////////// ARGUMENTS ////////////////////
    template< class ta_a >
    class vecarg
    {
        const ta_a& Argv;
    public:
        inline vecarg( const ta_a& A ) : Argv( A ) {}
        inline const float Evaluate( const int i ) const 
        { return Argv.Evaluate( i ); }
    };

    template<> 
    class vecarg< const float >
    {
        const ta_a& Argv;
    public:
        inline vecarg( const ta_a& A ) : Argv( A ) {}
        inline const float Evaluate( const int i ) const { return Argv; }
    };

    template<> 
    class vecarg< const int >
    {
        const ta_a& Argv;
    public:
        inline vecarg( const ta_a& A ) : Argv( A ) {}
        inline const float Evaluate( const int i ) const 
        { return (float)Argv; }
    };

//////////////////// EXPRESIONS ////////////////////
    template< class ta_a, class ta_b, class ta_eval >
    class vecexp_2
    {
        const vecarg<ta_a>   Arg1;
        const vecarg<ta_b>   Arg2;
    public:
        inline vecexp_2( const ta_a& A1, const ta_b& A2 )
         : Arg1( A1 ), Arg2( A2 ) {}
        inline const float Evaluate ( const int i ) const
        { return ta_eval::Evaluate( i, Arg1, Arg2 ); }
    };

    template< class ta_a, class ta_eval >
    class vecexp_1
    {
        const vecarg<ta_a>   Arg1;
    public:
        inline vecexp_1( const ta_a& A1 ) : Arg1( A1 ) {}
        inline const float Evaluate( const int i ) const
        { return ta_eval::Evaluate( i, Arg1.Evaluate( i ) ); }
    };

//////////////////// BASE CLASS ////////////////////
    template< int ta_dimension, class T >
    struct base : public T
    {
        inline const float Evaluate( const int I ) const 
        { return (*((T*)this))[i]; }
        //////////////////// ASSIGMENT ////////////////////
        template< class ta >
        inline const vector3d& operator = ( const ta& Exp )
        {
            for( int I=0; I<ta_ dimension; I++ )
                (*((T*)this))[I] = Exp.Evaluate( I );
        }
//////////////////// SUM ////////////////////
    struct sum
    {
        template< class ta_a, class ta_b > inline static 
        const float Evaluate( const int i, const ta_a& A, const ta_b& B )
        { return A.Evaluate(i) + B.Evaluate(i); }
    };

    template< class ta_c1, class ta_c2 > inline 
    const vecexp_2< const ta_c1, const ta_c2, sum > 
    operator + ( const ta_c1& Pa, const ta_c2& Pb )
    { return vecexp_2< const ta_c1, const ta_c2, sum >( Pa, Pb ); }

//////////////////// DATA ////////////////////

    struct desc_xyz
    {
        float X, Y, Z;      
        inline float& operator[](const int i) { return ((float*)this)[i]; } 
    };

    struct desc_xy
    {
        float X, Y;      
        inline float& operator[](const int i) { return ((float*)this)[i]; } 
    };
 
    struct desc_uv
    {
        float U, V;      
        inline float& operator[](const int i) { return ((float*)this)[i]; } 
    };
};

// Listing 6

Take a look at the source code in Listing 6. We have changed the name of our original vector3d to base. The namespace is now called vector. One nice thing is that now vecarg, vecexp, sum, and such are hidden from the global namespace. Our base class now takes two arguments, ta_dimension and class T, which allows us to build our own personalized vectors like in Listing 7. Note that we are forced to add the operator =. This is one thing about C++ that is not helpful sometimes. It seems that our original operator is unable to make it to its children. I haven’t sat down and worked out an elegant way to solve this.


struct vector3 : public vector::base< 3, vector::desc_xyz >
{
    typedef vector::base< 3, vector::desc_xyz > base; 

    inline vector3( const float x, const float y, const float z )
    { X = z; Y = y; Z = z; }

    template< class ta_type > inline
    vector3& operator = ( const ta_type& A )
    { base::operator = ( A ); return *this; }
};

 
struct vector2 : public vector::base< 2, vector::desc_xy >
{
    typedef vector::base< 2, vector::desc_xy > base;

    inline vector2( const float x, const float y )
    { X = x; Y = y; } 

    template< class ta_type > inline
    vector2& operator = ( const ta_type& A )
    { base::operator = ( A ); return *this; }
};

// Listing 7

Defining the compiler workarounds

Okay, we’re almost done. We now need to deal with Microsoft’s C++ compiler and make it do what we want. In our case we just want it to inline everything. For that, Microsoft has provided a few pragmas. If we fail to force the issue the compiler will try to be smart and fall on its face.


#pragma inline_depth( 255 )
#pragma inline_recursion( on )
#pragma auto_inline( on )

The first two pragmas tell the compiler to do inline recursion as deep as it needs to. You can change the depth to any number up to 255. The other pragma tells the compiler to inline whenever it feels like it. We want the compiler to inline all the functions. You would think that putting inline in front would do it, but that is not the case. The optimizer considers whether it’s worth inlining or not, which makes me wonder about the point of the inline keyword. We really need the optimizer not to think but just do. For that, Microsoft added another type of inline command called forceinline which tells the compiler to inline the functions no matter what. This almost works. I found myself having to “rebuild all” every time I compiled to force it to inline everything. Bad, bad Microsoft compiler! Finally, my last problem was that the compiler would not unroll the for loop that we introduced in the operator =. This may not be a big deal in the big picture, but it is just unacceptable for me. That is what got me madder that anything else. Well, this last problem also needs to be solved with templates.

Unrolling a loop with a template requires that you put the for loop in a recursive-like form. That is not a problem most times. I had to create two different structures in order to achieve my unroll. But it’s usually good enough with just one. To keep the compiler from recursing forever, I had to add a terminator. Look at Listing 8. This function, template<> struct recurse, tells the compiler not to use the generic template function, but to use this one instead. This is exactly the same thing that we did before with the vecarg class. The structure recurse has a function called assign. This function is where the guts of the for loop goes. In my case it’s just the assignment of one of the dimensions. The following line forces the recursion with this template structure. In the end, we just call our normal operator = and that takes care of everything. Interesting, right? In the program that comes with the article there are other examples of doing this trick with the dot product. Check it out.


template< class ta >
struct assigment
{
    template< int I, class R >
    struct recurse
    {
        enum{ COUNTER = I+1 };

        static inline void Assign( base<ta_dimension, T>& V, const ta& A ) 
        {
            V[I] = A.Evaluate( I );
            recurse<COUNTER, int>::Assign( V, A );
        }
    }; 

    template<> struct recurse<ta_dimension,int>
    {
        static inline void Assign( base<ta_dimension, T>& V, const ta& A ) {}
    };
 
    static inline void Assign( base<ta_dimension, T>& V, const ta& A )
    {
        recurse<0,int>::Assign( V, A );
    }
};

 
template< class ta_type > inline
const base<ta_dimension, T>& operator = ( const ta_type& A )
{
    assigment<ta_type>::Assign( *this, A );
    return *this;
}

// Listing 8

Examining the results

And now the critical question: How fast is it really? I implemented three versions of the vector math routines. The first version is based on Jim Blinn’s article, the second version is mine, and the last version is the common method. The graph shows the performance on an AMDK7 950Mhz. The thing that surprised me the most from the results was that my version worked faster than Jim’s. It has nothing to do with the concepts, but rather how the compiler chose to inline. At the end of the day both Jim’s version and my version should have ended up working at the same speed, but the universe is not perfect.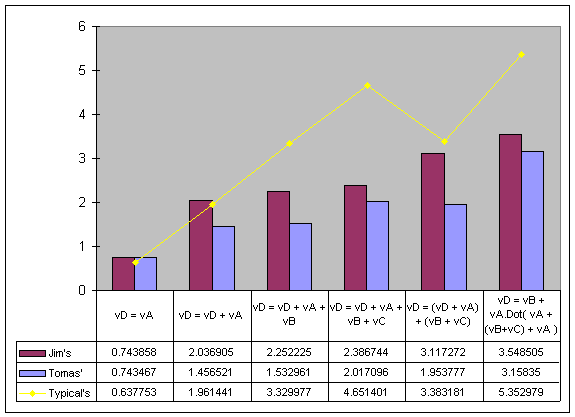

VD = vD + vA + vB

vD = vD + vA + vB


mov   ecx,dword ptr ds:[408C68h]
mov   edx,dword ptr ds:[408C6Ch]
mov   dword ptr [ebp-24h],ecx
fld   dword ptr [ebp-24h]
mov   ecx,dword ptr ds:[408C70h]
mov   dword ptr [ebp-20h],edx
mov   edx,dword ptr ds:[408C78h]
mov   dword ptr [ebp-18h],edx
mov   edx,dword ptr ds:[408C80h]
fadd  dword ptr [ebp-18h]
mov   dword ptr [ebp-1Ch],ecx
mov   ecx,dword ptr ds:[408C7Ch]
fadd  dword ptr ds:[408C88h]
mov   dword ptr [ebp-14h],ecx
mov   dword ptr [ebp-10h],edx
fstp  dword ptr ds:[408C68h]
fld   dword ptr [ebp-20h]
fadd  dword ptr [ebp-14h]
fadd  dword ptr ds:[408C8Ch]
fstp  dword ptr ds:[408C6Ch]
fld   dword ptr [ebp-1Ch]
fadd  dword ptr [ebp-10h]
fadd  dword ptr ds:[408C90h]
fstp  dword ptr ds:[408C70h]


fld   dword ptr ds:[408CE8h]
fadd  dword ptr ds:[408CD8h]
mov   dword ptr [ebp-14h],edx
mov   dword ptr [ebp-10h],eax
fadd  dword ptr ds:[408D08h]
fstp  dword ptr ds:[408D08h]
fld   dword ptr [eax+4]
fadd  dword ptr ds:[408CECh]
fadd  dword ptr ds:[408D0Ch]
fstp  dword ptr ds:[408D0Ch]
fld   dword ptr [eax+8]
fadd  dword ptr ds:[408CF0h]
fadd  dword ptr ds:[408D10h]
fstp  dword ptr ds:[408D10h]


fld   dword ptr ds:[408C98h]
fadd  dword ptr ds:[408CC8h]
fld   dword ptr ds:[408C9Ch]
fadd  dword ptr ds:[408CCCh]
fstp  dword ptr [ebp-8]
fld   dword ptr ds:[408CA0h]
fadd  dword ptr ds:[408CD0h]
fstp  dword ptr [ebp-4]
fadd  dword ptr ds:[408CA8h]
fstp  dword ptr [ebp-18h]
fld   dword ptr [ebp-8]
mov   edx,dword ptr [ebp-18h]
fadd  dword ptr ds:[408CACh]
mov   dword ptr ds:[408CC8h],edx
fstp  dword ptr [ebp-14h]
fld   dword ptr [ebp-4]
mov   ecx,dword ptr [ebp-14h]
fadd  dword ptr ds:[408CB0h]
mov   dword ptr ds:[408CCCh],ecx
fstp  dword ptr [ebp-10h]
mov   edx,dword ptr [ebp-10h]
mov   dword ptr ds:[408CD0h],edx

Jim’s

Tomas’

Typical’s

Let’s take a quick look at some of the assembly generated by each of the versions. You will notice that Jim’s code is actually the longest, yet it performs better than the standard method. The compiler produced code which stalled less than the common implementation. It accomplishes this by interleaving the moves and the floating point operations. You can still see how much movement of memory there is due to poor inlining. My method had some memory movement, but far less than either of the other two versions. The common method fails to inline as much as it should, and spends most of its time moving memory from the floating point unit. Although performance may vary with different compiler options, Jim’s and mine should most often produce better code.

Limitations

In a statement like vA = vB + vC, each component of vA can be expressed using only one component each from vB and vC. However, assume we have a cross product function and the following: vA = Cross( vB, vC ). There is no way to express, say, vA.X using only one component from vB (or from vC). This last one isn’t too bad. But it can get much worse. Consider: vA = Cross( vB1+vB2, vC1+vC2 ). The two vector adds should need 6 floating point additions total, and the cross product itself needs 3 subtractions. But beware! A naïve implementation of the cross product using these techniques could very well end up performing 12 floating point additions and 3 subtractions. Dot products can also lead to trouble. I the source code included with this article there is an example on how to implement the Dot product properly.

A colleague of mine, D. Michael Traub, pointed out, it gets even worse if you extrapolate these techniques to matrices. Consider matrix concatenation: mA = mB * mC. The upper left cell of mA can only be expressed by using 4 components each from mB and mC. Of course, matrix transposition does not have any problems since each cell of the transposed matrix is expressed as one cell from the original matrix. It’s just not the same cell.

These techniques work best when each component of the resulting vector can be expressed entirely in terms of only one component per vector in the expression. Operations which are troublesome should just do it the old fashioned way and fully compute their result to be stored internally. Our clever “solve completely for each component at a time” pipeline will be forced to stall on these operations, but it certainly beats redundant computations.

Conclusion

Well, we have learned to take a simple math vector class and transmute it into a mean parsing machine. With three dimensional vectors, we realized performance improvements of up to 2.3 times over the typical implementation. There should be even larger gains with vectors of higher dimensions. (Note that there was no attempt to implement template versions of matrix operations, so we don’t know where that may lead or what performance changes may be realized. Said differently, the matrix version is left as a reader exercise!)

As cool as this all sounds, it has its place. There are many issues with using templates. Most compilers still don’t completely satisfy the standard C++ language description. This can cause incompatible code, not to mention obfuscated bugs. There is the issue with the optimizer and the inlining. Not all compilers can do this in a very elegant way. The Microsoft compiler wouldn’t inline everything unless I rebuilt the entire project. There are also the new SIMD instructions in the new processors which provide an attractive alternative to using standard floating point math for our vectors. But all is not lost. We have learned how to think in a different way using templates. We can apply our new knowledge to many other problems such as AI, physics, or even file processing. As always, it is up to you to decide whether this new tool is the right thing for a particular problem. So pick and choose your battles carefully, because there are two times you need to deal with: run time and development time.

Download the source code included with this article: article_fastervectormath.zip

References

Tomas Arce
www.zen-x.net

Jim Blinn
Jim Blinn’s Corner. Optimizing C++ vector Expressions
IEEE Computer Graphics Applications
www.research.microsoft.com/~blinn/

Pete Isensee
Fast Math Using Template Metaprogramming
Game Programming Gems