|
Coding Bloom Filters by (11 September 2000) |
Return to The Archives |
The Story
 |
| It never pays to be before your time. It is also not helpful if the trend of technology is marching away from you. This would be the actual outcome of a simple and clever algorithm which is believed to be first published by Burton H. Bloom in the Communications of the ACM in 1970 ( Volume 13 / Number 7 / July 1970 ). While actually authored in 1969, at a time close to the initial conceptions of the early ARPA network, it would take almost 25 years before the modern commercial internet would bring back the practical use of Bloom's idea. However, between these times, most of the characteristics of mainframe and desktop systems would make Bloom's efforts less relevant. Most people are surprised at the simplicity of this algorithm. It is obvious how the Bloom filter works. It is not obvious how well the Bloom filter works. |
The Scenario
 |
| Imagine, if you will, the desire to store boolean information in a bit array. A very simple premise. You simply assign each element in the bit array to a meaning and then assign it a value. In this scenario, it takes 1 bit in the array to store 1 bit of stored information. The bit array faithfully represents its appropriate value with 100 percent accuracy. This, of course, works best when the stored data is array oriented like a transient over time or space. But what if the data you wish to store is not a linear transient oriented dataset? |
Bloom's Way
 |
| In his publication, Bloom suggests using a "Hash coding with Allowable Errors" algorithm to help word processors perform capitalization and/or hyphenation on a document. An algorithm that could use less space and be faster than a conventional one to one mapping algorithm. In both of these example cases, a majority of words ( 90+% for example ) could be checked using a simple rule, while the smaller minority set could be solved with special cases and an exception list used to catch the instances where the algorithm would report a word as simply solvable when it was not. His motivation was to reduce the time it took to lookup data from a slow storage device to faster 'core memory'. At the time, is was unlikely typical memory systems could hold the entire ruleset for such a task in system memory. Blooms way could dramatically improve the performance with existing hardware. |
Enter The Game Designer
 |
Assumed facts:In this example we will use Bloom's algorithm to store the existence of these triggers in a bit array. This bit array will be created on the server and downloaded to each client. The clients will have the possibility of returning a false positive when accessing the bit array so we will always access the server for final verification and to extract more details about the trigger. Each time the clients avatar position changes, we will interrogate the bit array using the X, Y, & Z position information to determine if a position based trigger has been activated. We can also query the bit array with avatars posessions and position to search for item related triggers. The range of tests are unlimited so use your imagination. Testing the bit array is cheap: A Pentium II 400 MHZ can do about 10,000 per second with unoptimized code). The Bloom filter will tell us if a trigger has been activated with a decent degree of accuracy. This false positive case is acceptable as long as the false positive rate is low, because for each TRUE case we get back from the Bloom filter, we will hit the server to get the actual trigger information. |
How It Works
 |
To store the status of a trigger in a Bloom bit array N bits long, take the
triggers input test cases and produce a high quality hashed number. Then, take
the first N bits from the result of the hashed number and set the index N in the
bit array to TRUE. 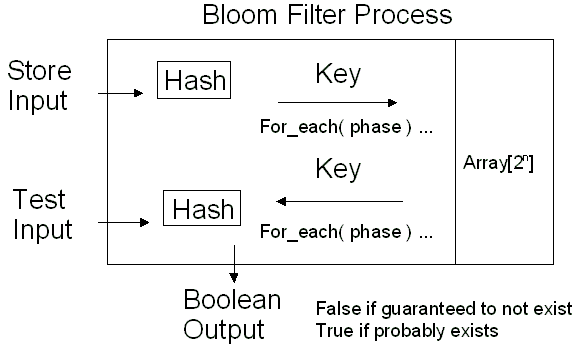 We repeat this about 5 to 20 times setting 5 to 20 bits, respectively, in the bit array using the next consecutive N bits from the hashed output. The bit array starts out reset ( FALSE ), before we start to populate the bit array with data. As the array becomes more populated, sometimes we will set a bit that has already been set. This is the root of the false positive cases. When we wish to examine the trigger existence for a specific input case, we proceed in almost the exact steps except we read the bits from the bit array instead of setting them. If any of the bits are zero ( FALSE ), the trigger is guaranteed to not exist. If all of the bits are set ( TRUE ), the trigger is likely to exist and the server should be queried for a precise answer and to obtain trigger details. |
Tuning The Bloom Filter
 |
|
The saturation is defined to be the percent of bits set to TRUE
in the bit array.
The phase is defined to be
the number of times we attempt to set a bit in the array ( 5 to 20
times in this example ). false_positive_rate = saturationphase Both of these variables can be modified to change the accuracy and capacity of the Bloom filter. Generally speaking, the larger the size of the bit array (N) and the higher the phase, the less likely a false positive response will occur. Bloom asserted that the optimum performance of this algorithm occurs when saturation of the bit array is 50%. array_size = (phases * max_inputs)/-LN(0.5) Statistically, the chance of a false positive can be determined by taking the saturation and raising it to the power of the phase. Other equations are also available to help tune the Bloom filter algorithm. |
Extra Unintended Benefits
 |
| While not super secure, this algorithm has the additional unintented effect of obfuscating the true existence of triggers. The bit array sent to the client machine will be mostly random if the bit array is optimized well for its stored capacity. And someone would need to iterate (232)3 times to examing all possible inputs for int X, int Y & int Z to find all triggers. |
Extra Facts
 |
|
|
Closing
 |
|
Authored by
Mark Fischer @
Beach Software
About the Author Mark Fischer is an independent consultant specializing in XML & high speed internet applications. When not consulting, Mark is busy working on a very cool unannounced product. additional references: Bloom Filters @ beach Software Norman Hardy on Bloom Filters |
|
|