|
3D Graphics on Mobile Devices - Part 3: Polygon Graphics by (24 August 2003) |
Return to The Archives |
Introduction
 |
| This is the third part of the series of articles on 3D graphics for mobile devices. In the previous article I described how to use fixed point mathematics to do accurate calculations on devices that lack an FPU, like Symbian devices and PocketPCs. In this article, I will describe the 3D engine that I am currently developing for Overloaded, a manufacturer and distributor of games for mobile devices. |
Another Engine?
 |
|
Because of the lack of an FPU, it's not easy to port an engine to Symbian (or PocketPC). There is a port of Quake for PocketPC, based on the original sourcecode, but it runs at 5-12fps, despite the fact that the original ran fine on a P90 machine. This is because the port makes heavy use of floating point calculus, and emulated floating point code runs at about 5% of the speed of an FPU. It's clear that an engine developed specifically for mobile devices makes sense. There are some commercial engines available, but these are quite expensive. Besides, they have their disadvantages, like big codebases (we distribute our software over the air, so we like to keep it under 250Kb) or bad accuracy (check out Tombraider on a PDA). It's not hard to do a relatively good job in a short timespan. I promised my employer to deliver a basic 3D engine in less than 2 months, with the following features: This is of course a very basic list. Obviously, some things are missing that are needed to use the engine for a game, such as collision detection and physics. We decided to implement all features beyond 'basic functionality' on-demand. |
Scene Graph
 |
|
Those of you familiar with my previous work will know that I used to build my engine on top of some form of spatial subdivision scheme. Basically I would store polygons in an octree or kd-tree of some form. Well, I have changed my mind. Spatial subdivisions are still the way to go if you want performance that does not depend on overall scene size. However, these structures are not suitable as a basis for scene data. While they do subdivide space, they do not deal with object relations. For my previous job (at Davilex Software), I worked quite a bit with the NetImmerse 3D engine. The core of this engine is a scenegraph: A tree-like structure that represents the game world and the relations between objects in the world. Imagine a city (root node) with cars driving around in it (childs of the roodnode) and moving wheels on the cars (childs of the car nodes). Storing this scene in the scenegraph is very intuitive. Besides, the way scenes like these are rendered, using concatenated transformation and translation matrices, matches the structure very well. You gotta love the beauty of scene graphs. NetImmerse takes the whole concept a bit further: You can put all sorts of things in the scenegraph, like cameras and lights, rendering properties, animation stuff and so on. While that's currently beyond the scope of what we need, it's good to know that there's plenty of room for expansion. 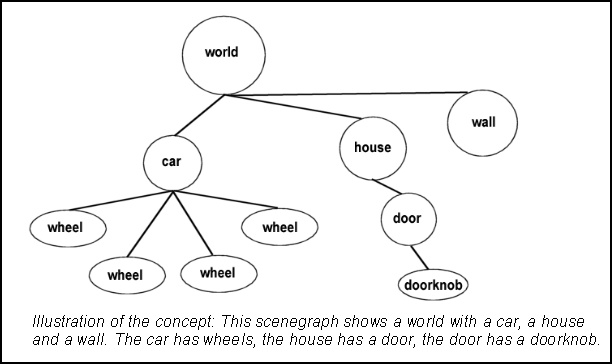 So, I decided to implement a simple scene graph. The main structure is called 'World' in my 3D engine. The world has one root node. Each node, including the root, can have any number of child nodes. A node has a matrix and can have zero or one meshes; when a node has no meshes, it's apparently only created to group a couple of meshes or nodes. A mesh refers to polygons and a texture. Polygons refer to vertices. A vertex has an UV-coordinate and a coordinate, wich holds the position in object space, the transformed position (in camera space) and the projected coordinates (in screen space). That's the data structure in a nutshell. Note that the engine uses polygons with 3-10 vertices. There are a lot of good reasons for this: Each edge needs a couple of divisions during rasterization; you have to interpolate 'x', and probably also 'u' and 'v'. A quad thus saves at least two divisions compared to two triangles. There are less horizontal spans to be rendered, and although you still draw the same number of pixels, you can skip a lot of (expensive) setup code. Quads look better than triangles. When drawing triangles, you will notice that all spans are not only parallel in screenspace, but also in texturespace. While this can be exploited to save a lot of divisions, it also emphasizes the artifacts of affine texturemapping (as opposed to perspective correct texture mapping). Larger polygons can be stored more efficiently and make simpler BSP trees. And finally: Fewer polygons means faster collision detection. |
Importing
 |
|
Initially, I used AC3D as a modelling package. AC3D is similar to MilkShape, but offers a bit more functionality. Like MilkShape, AC3D is a modelling package that is targeted at low polygon modelling. AC3D can export polygons with more than 3 vertices, but it's hard to merge triangles manually, so I wrote a converter that takes an AC3D file and prepares it for the 3D engine. The converter merges polygons, aligns normals, generates BSP trees and compresses the final data. Right now we have a real artist on the racer, and he's not exactly satisfied with the editing in AC3D. Instead, he builds the tracks in 3D Studio Max, then exports them to AC3D, which exports them to the engine. AC3D now serves as a filter: It forces the artist to deliver clean data and gives a pretty good impression of how the scene will look in the renderer. |
Visibility Determination
 |
|
The first game using the 3D engine is a racing game. The tracks consist of a number of 'chunks' (about 25 per track) and some scenery objects. The total number of objects in the scene graph will thus be less then 50. We decided to keep the visibility determination extremely simple: Each mesh has a bounding sphere, and this sphere is tested against the view frustum. Doing this 50 times to render a frame is no problem at all. This 'algorithm' can be improved slightly by keeping track of hierarchical bounding spheres: A hierarchical bounding sphere is a sphere that contains not only it's own node, but also the nodes attached to that node. It's the sphere that contains a branch of the scene graph. An interesting feature of this sphere is that when a frustum plane does not intersect it, the nodes below the current one do not need to be tested against it anymore. This often eliminates half or more of the sphere-to-plane tests. There's a catch: You need to keep track of the bounding spheres. When you modify the position or orientation of a node, you need to check whether this has an impact on one of the hierarchical bounding spheres of one of the parents of the node. |
Physics
 |
| For the physics of the cars, I consulted Marco Monster. Well, his website, at http://home.planet.nl/~monstrous/tutcar.html. He has an excellent article on the subject, and describes in pretty much detail what forces affect a car. |
Collision Detection
 |
|
To detect collisions of the car and the scenery, I use the bounding sphere of the car. This sphere is tested against the bounding spheres of the objects in the scenegraph. Whenever the spheres overlap, the bounding sphere of the car is tested against the triangles in the mesh. When a collision occurs, the car is displaced so that it no longer penetrates the surface, and it's velocity vector is adjusted so that it slides along the triangle that it collided with. Testing a sphere against a triangle is a tricky operation. There is some code available on the web that does this for triangles, but I'm using larger polygons too, so I needed a more generic approach. I finally found a good approach that uses a number of steps to determine wether or not a sphere and a polygon collide: First, check if the sphere intersects the plane of the polygon. This cheaply eliminates a lot of polygons (one dot product). Secondly, check if the center of the bounding sphere is inside the polygon (point-in-polygon test). If this is the case, there's contact. If this is not the case, we are not sure that there is no contact, so we need to check the edges of the polygon against the sphere (line segment / sphere intersection). After this, we have a conclusive yes or no. I found that collision detection is pretty fast this way, it is no problem to check the car against every object in the scene, or even against another car (200+ polygon objects). |
Shadows
 |
The car in the racer has a basic shadow, that adds a lot to the atmosphere nevertheless. The shadow is the convex outline of a rectangular shape with the corners cut off, merged with an identical shape, this time displaced according to the position of the lightsource. This definitely needs a picture: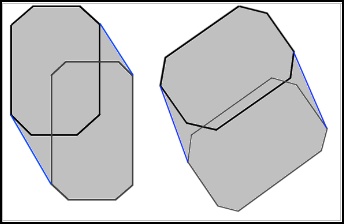 This shadow works remarkably well, although it has no real resemblance with the shape of the car. The difference between this and a basic dropshadow is that this one changes when the orientation of the car changes, or when the sun is moved. It can also reflect sunsets, by placing the two convex shapes further apart. |
Controls
 |
| The phones have very limited controls. On the Nokia 7650, there's a tiny joystick, but it gives you a sore thumb in no time, and it doesn't seem to allow for diagonal movements. So using the throttle and the steer simultaneously is not going to work. We will try two control schemes: The first one allows you to modify the throttle and steer but doesn't let go of the throttle unless you deliberately push back the joystick. That way, you can steer at full speed. The second scheme is much simpler: The throttle depends on your alignment with the road. When you are well aligned, the car speeds up, otherwise it slows down. You will still need a key to reverse in case of a collision, but besides that, the game is playable with just a 'left' and 'right' button. Hardly realistic, but I believe playability should have precedence over realism. We are considering to make this an option, so that the player can decide. To keep multiplayer races fair, you should have a slight advantage when using 'manual' control compared to 'automatic' control. This seems to work well in other racing games. |
Conclusion
 |
|
I met the two month deadline on this project by keeping things simple and reusing good ideas from engines that I wrote myself and engines that I worked with. I also took good snippets of code from the web, like the collision detection code. The result is a robust, extensible engine. You can check out a demo of it powering an early version of the race game by clicking here (578k). Next time I will discuss the software rasterizers of the 3D engine. Have fun - Keep coding. - Jacco Bikker, a.k.a. "The Phantom" |
|
Article Series:
|